Answer:
a) [20.366, 31.834]
b) Since, The age of 35 years does not belongs to the calculated interval of 95% confidence interval (i.e [20.366, 31.834]).
Paul's age is significantly different from his Mean Wii Fit Age.
Explanation:
Data provided:
Number of days i.e sample size, n = 7
Mean, μ = 26.1
Standard deviation, σ = 6.2
Degrees of freedom, df = n - 1 = 7 - 1 = 6
Confidence level = 95%,
Now,
For Confidence level of 95% , α = 1 - 0.95 = 0.05
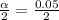 = 0.025,
= 0.025,
From the t stats table,
tc = t(α/2, df)
or
tc = t(0.025, 6) = 2.447
Therefore,
Margin of error =
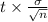
or
Margin of error =

or
Margin of error = 5.734
Therefore,
The 95% confidence interval = Mean ± Margin of error
or
The 95% confidence interval = [ (26.1 - 5.734) , (26.1 + 5.734)]
or
The 95% confidence interval = [20.366, 31.834]
b) Since, The age of 35 years does not belongs to the calculated interval of 95% confidence interval (i.e [20.366, 31.834]).
Therefore, it can be concluded that the Paul's age is significantly different from his Mean Wii Fit Age.