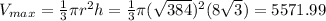Question

Among all right circular cones with a slant height of 24​, what are the dimensions​ (radius and​ height) that maximize the volume of the​ cone? The slant height of a cone is the distance from the outer edge of the base to the vertex. Let V be the volume of the cone. What is the objective function in terms of the height of the​ cone, h?

Answer 1

5571.99

Explanation:

We need to use the Pythagorean theorem to solve the problem.

The theorem indicates that,

`r^2+h^2=24^2 \\r^2+h^2=576\\r^2=576-h^2`

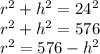
Once this is defined, we proceed to define the volume of a cone,

`v=(1)/(3)\pi r^2 h`

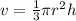
Substituting,

`v=(1)/(3) \pi (576-h^2)h\\v=(1)/(3) \pi (576h-h^3)`

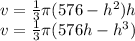
We need to find the maximum height, so we proceed to calculate h, by means of its derivative and equalizing 0,

`(dv)/(dh) = (1)/(3) \pi (576-3h^2)`

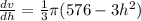
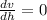`(dv)/(dh) = 0` then
`\rightarrow (1)/(3)\pi(576-3h^2)=0`

`h_1=-8√(3)\\h_2=8√(3)`

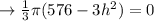
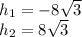
We select the positiv value.

We have then,

`r^2 = 576-(8\sqrt3)^2 = 384\\r=√(384)`

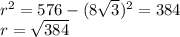
We can now calculate the maximum volume,

`V_(max)= (1)/(3)\pi r^2 h = (1)/(3)\pi (√(384))^2 (8√(3)) = 5571.99`