Question

There are three executives in an office, ages 56, 57, and 58. If a 57-year-old executive enters the room, the

a.The mean age will stay the same but the variance will increase.
b.The mean age and variance will stay the same.
c.The mean age will stay the same but the variance will decrease.
d.The mean age and variance will increase.

Answer 1

option (c) The mean age will stay the same but the variance will decrease

Explanation:

Case I: For 3 executives of ages 56, 57 and 58

Number of executives, n = 3

Mean =
`\frac{\textup{56 + 57 + 58 }}{\textup{3}}`

or

Mean = 57

Variance =
`\frac{\sum{(Data - Mean)^2}}{\textup{n-1}}`

or

Variance =
`\frac{(56 - 57)^2+(57-57)^2+(58-57)^2}{\textup{3-1}}`

or

Variance =
`\frac{1+0+1}{\textup{2}}`

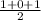
or

Variance = 1

For Case II: For 4 executives of ages 56, 57, 58 and 57

Number of executives, n = 4

Mean =
`\frac{\textup{56 + 57 + 58 + 57 }}{\textup{4}}`

or

Mean = 57

Variance =
`\frac{\sum{(Data - Mean)^2}}{\textup{n-1}}`

or

Variance =
`\frac{(56 - 57)^2+(57-57)^2+(58-57)^2+(57-57)^2}{\textup{4-1}}`

or

Variance =
`\frac{1+0+1+0}{\textup{3}}`

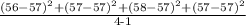
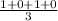
or

Variance = 0.67

Hence,

Mean will remain the same and the variance will decrease

Hence,

The correct answer is option (c) The mean age will stay the same but the variance will decrease