Question

As many as 20% of all Americans contract influenza each year. A sample of 400 randomly selected Americans is chosen and the number with influenza is recorded. Let X represent the number with influenza in the sample. What is the probability that at least 25% of the sample is observed to have influenza?

Answer 1

Answer: 0.0062

Explanation:

Let X represent the number with influenza in the sample.

As per given , we have

p= 0.20

n= 400

then,

`\mu=np=400\cdot0.20=80\\\\\sigma=√(np(1-p))\\\\=√(400(0.2)(0.8))=8`

`x=400\cdot0.25=100`

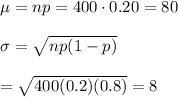
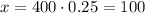
z-score :
`z=(x-\mu)/(\sigma)`

`z=(100-80)/(8)=2.5`

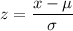
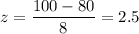
The probability that at least 25% of the sample is observed to have influenza:

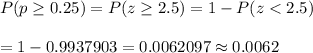`P(p\geq0.25)=P(z\geq2.5)=1-P(z<2.5)\\\\=1-0.9937903=0.0062097\approx0.0062` [using p-value calculator ]

Hence, the probability that at least 25% of the sample is observed to have influenza = 0.0062