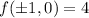Question

Find the extreme values of the function f(x, y) = 4x2 + 6y2 on the circle x2 + y2 = 1.

Answer 1

Answer with Step-by-step explanation:

We are given that

`f(x,y)=4x^2+6y^2`

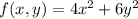
Let g(x,y)=
`x^2+y^2=1`

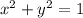
We have to find the extreme values of the given function

`\\abla f(x,y)<8x,12y>`

`\\abla g(x,y)=<2x,2y>`

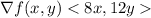
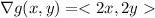
Using Lagrange multipliers

`\\abla f(x,y)=\lambda \\abla g(x,y)`

`f_x=\lambda g_x`

`8x=\lambda 2x`

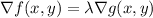
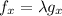
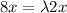
Possible value x=0 or
`\lambda=4`

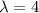
If x=0 then substitute the value in g(x,y)

Then, we get
`y=\pm 1`

`f_y=\lambda g_y`

`12y=\lambda 2y`

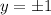
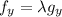
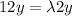
If
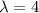`\lambda=4` and substitute in the equation

Then , we get possible value of y=0

When y=0 substitute in g(x,y) then we get

`x=\pm 1`

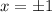
Hence, function has possible extreme values at points (0,1),(0,-1), (1,0) and (-1,0).

`f(0,1)=6`

`f(0,-1)=6`

`f(1,0)=4`

`f(-1,0)=4`

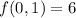
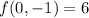
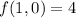
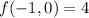
Therefore, the maximum value of f on the circle
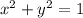`x^2+y^2=1` is
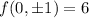`f(0,\pm1)=6` and minimum value of
`f(\pm1,0)=4`