Answer:
Critical points are 1 and -1
Maximum at x=1
Minimum at x=-1
Explanation:
We are given that a function
 on (
on (
 )
)
We have to find the critical points of the function.
To find the critical point we will differentiate function w.r.t x and then substitute f'(x)=0
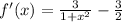

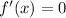
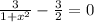



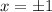
Therefore, the critical points of the given function are 1 and -1.
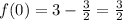
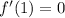
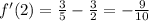
When we goes from 0 to 2 then the sign of derivative change from positive to negative .Therefore, function has local maximum at x=1.
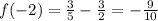
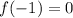
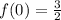
When we goes form -2 to 0 then the sign of derivative change from negative to positive .Hence , function has local minimum at x=-1
Hence, critical points are local maximum and local minimum .