Question

The owner of Chips etc. produces two kinds of chips: lime (L) and vinegar (V). He has a limited amount of the three ingredients used to produce these chips available for his next production run: 4800 ounces of salt, 9600 ounces of flour, and 2000 ounces of herbs. A bag of lime chips requires 2 ounces of salt, 6 ounces of flour, and 1 ounce of herbs to produce; while a bag of vinegar chips requires 3 ounces of salt, 8 ounces of flour, and 2 ounces of herbs. Profits for a bag of lime chips are $0.40, and for a bag of vinegar chips $0.50. What is the formulation for this problem? Suppose that L and V are the decision variables respectively of Lime and Vinegar.

Answer 1

Objective function (maximize)

`Profit=0.40L+0.50V`

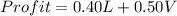
Constraints

- Availabitily of salt:
`2L+3V\leq4800`

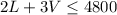
- Availability of herbs:
`1C+2V\leq 2000`

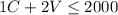
- Availability of flour:
`6C+8V\leq9600`

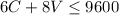
Step-by-step explanation:

This a linear programming problem. We have an objective function (in this case it is the profit) that we want to optimize, but complying with constraints (in this case, the availability of ingredients).

The objective function can be defined taking into account the profits of the two kind of chips:

`Profit=0.40L+0.50V`

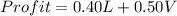
The constraints can be expressed taking into account the amount of ingredients every unit of chip needs and stating that it has to be less or equal to the availability of this ingredient:

- Availabitily of salt:

`2L+3V\leq4800`

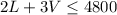
- Availability of herbs

`1C+2V\leq 2000`

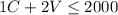
- Availability of flour

`6C+8V\leq9600`

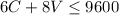
With these expressions the linear programming problem can be solved.