Answer:
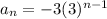 ; {-3,-9, -27,- 81, -243, ...}
; {-3,-9, -27,- 81, -243, ...}
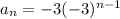 ; {-3, 9,-27, 81, -243, ...}
; {-3, 9,-27, 81, -243, ...}
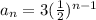 ; {3, 1.5, 0.75, 0.375, 0.1875, ...}
; {3, 1.5, 0.75, 0.375, 0.1875, ...}
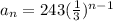 ; {243, 81, 27, 9, 3, ...}
; {243, 81, 27, 9, 3, ...}
Explanation:
The first explicit equation is
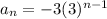
At n=1,

At n=2,
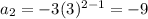
At n=3,
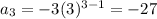
Therefore, the geometric sequence is {-3,-9, -27,- 81, -243, ...}.
The second explicit equation is
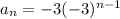
At n=1,
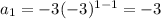
At n=2,
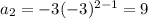
At n=3,
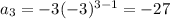
Therefore, the geometric sequence is {-3, 9,-27, 81, -243, ...}.
The third explicit equation is
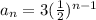
At n=1,
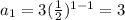
At n=2,
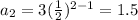
At n=3,
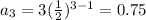
Therefore, the geometric sequence is {3, 1.5, 0.75, 0.375, 0.1875, ...}.
The fourth explicit equation is
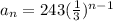
At n=1,
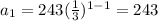
At n=2,
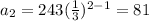
At n=3,
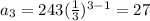
Therefore, the geometric sequence is {243, 81, 27, 9, 3, ...}.