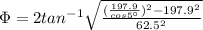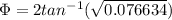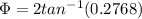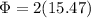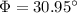Question

The solid right-circular cylinder of mass 500 kg is set into torque-free motion with its symmetry axis initially aligned with the fixed spatial line a–a. Due to an injection error, the vehicle’s angular velocity vector ω is misaligned 5◦ (the wobble angle) from the symmetry axis. Calculate to three significant figures the maximum angle φ between fixed line a–a and the axis of the cylinder.

Answer 1

30.95°

Step-by-step explanation:

We need to define the moment of inertia of cylinder but in terms of mass, that equation say,

`A=(1)/(12)m(3r^2+l^2)`

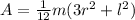
Replacing the values we have,

`A=(1)/(12)(500)(3(0.5)^2+(2)^2)`
`A=197.9kg.m^2`

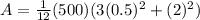
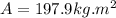
At the same time we can calculate the mass moment of intertia of cylinder but in an axial way, that is,

`c=(1)/(2)mr^2`

`c=(1)/(2)(500)(0.5)^2`

`c=62.5kg.m^2`

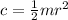
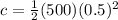
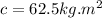
Finally we need to find the required angle between the fixed line a-a (I attached an image )

`\Phi = 2tan^(-1)\sqrt{(((A)/(cos\gamma))^2-A^2)/(c^2)}`

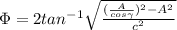
Replacing the values that we have,

`\Phi = 2tan^(-1)\sqrt{(((197.9)/(cos5\°))^2-197.9^2)/(62.5^2)}`

`\Phi = 2tan^(-1)(√(0.076634))`

`\Phi = 2tan^(-1)(0.2768)`

`\Phi = 2(15.47)`

`\Phi = 30.95\°`