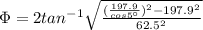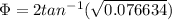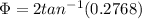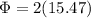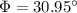Answer:
30.95°
Step-by-step explanation:
We need to define the moment of inertia of cylinder but in terms of mass, that equation say,
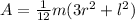
Replacing the values we have,
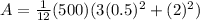
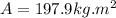
At the same time we can calculate the mass moment of intertia of cylinder but in an axial way, that is,
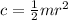
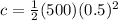
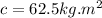
Finally we need to find the required angle between the fixed line a-a (I attached an image )
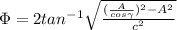
Replacing the values that we have,