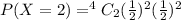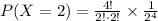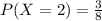Answer:0.375
Step-by-step explanation:
Given
An Urn contains 3 White and 3 black balls
Ball is replaced after it is drawn
Using Binomial Distribution as trials are finite
n=4 i.e. 4 balls are drawn
Probability of getting white ball

Probability of getting a Non-white ball
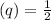
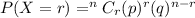
For Exactly 2 white balls