Which represents the solution(s) of the system of equations, y + 4 = x2 and y-x=2? Determine the solution set by graphing (-2, 0) (-2, 0) and (2,0) (-2, 0) and (3,5) no solution…

Question

asked May 14, 2020 150k views

2 Answers

KennethLazos · Answer 1 · 2020-05-18T04:55:05+0000

Answer:

The points (-2, 0) and (3,5) are the ONLY solutions of the given sets of equations.

Explanation:

Here, the given equations are:
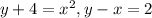
y + 4 = x^(2) , y -x = 2

Now checking for the given points:

(a) (-2, 0)

Here,
$y + 4 = 0 + 4 = 4 =   (-2)^(2)  =  x^(2) \\y- x = 0 -(-2) = 2  = RHS$

Hence, (-2, 0) is the solution of the given equations.

b) Checking for (2,0), as (-2, 0) is a solution as shown above

Here,
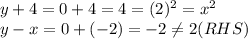
$y + 4 = 0 + 4 = 4 =   (2)^(2)  =  x^(2) \\y- x = 0 +  (-2) = -2  \\eq 2(RHS)$

Hence, (2, 0) is NOT the solution of the given equations.

c) Checking for (3,5), as (-2, 0) is a solution as shown above

Here,
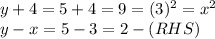
$y + 4 = 5 + 4 = 9 =   (3)^(2)  =  x^(2) \\y- x = 5 -3 = 2 -  (RHS)$

Hence, (3,5), is the solution of the given equations.

Hence, the points (-2, 0) and (3,5) are the ONLY solutions of the given sets of equations.