The value of
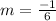 and
and

Solution:
Given, Line passes through points
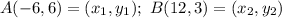
Slope of line passing through two points is

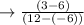

Equation of a straight line passing through point-slope form is
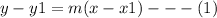
Since we have two points we can use any point. Let us take
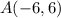 and m
and m
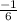 and substitute in (1)
and substitute in (1)
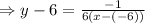

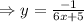 [By equating as
[By equating as
 ]
]

Substituting the other coordinates also gives the same result.