Question

A hot-air balloon descends from a height of 2000 feet for 40 seconds. The function models the height of the hot-air balloon during this descent, where t is the amount of time since the descent began. What is the practical domain of the function in this situation? What is the practical range of the function in this situation?

Answer 1

The domain is all real values greater than or equal to 0 seconds and less than or equal to 40 seconds

The range is all real values greater than or equal to 0 feet and less than or equal to 2,000 feet

Explanation:

Let

t ----> is the amount of time since the descent began

f(t) ---> is the height of a hot-air balloon descends

we know that

The linear equation in slope intercept form is equal to

`y=mx+b`

where

m is the unit rate or slope of the linear equation

b is the y-intercept or initial value

In this problem we have that

The slope or unit rate is equal to

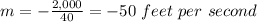`m=-(2,000)/(40)=-50\ feet\ per\ second` ---> is negative because is a decreasing function

The y-intercept or initial value is equal to

`b=2,000\ ft`

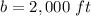
substitute

`f(t)=-50t+2,000`

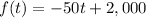
The domain is the interval -----> [0,40]

`0\leq t\leq 40`

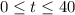
All real values greater than or equal to 0 seconds and less than or equal to 40 seconds

The range is the interval ----> [0,2,000]

`0\leq f(t)\leq 2,000`

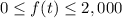
All real values greater than or equal to 0 feet and less than or equal to 2,000 feet