Answer:
The 99% confidence interval for the population mean is 22.96 to 26.64
Explanation:
Consider the provided information,
A sample of 49 customers. Assume a population standard deviation of $5. If the sample mean is $24.80,
The confidence interval if 99%.
Thus, 1-α=0.99
α=0.01
Now we need to determine

Now by using z score table we find that
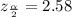
The boundaries of the confidence interval are:
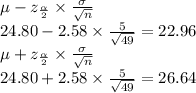
Hence, the 99% confidence interval for the population mean is 22.96 to 26.64