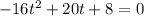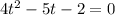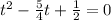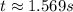Answer:
(a)0.625s (b)1.569s
Step-by-step explanation:
a.The ball reaches its maximum height when its speed = 0, or changing from positive to negative. To find out the time t for this we need to get the velocity function by taking the first derivative of the height function:
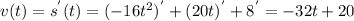
So when v(t) = 0

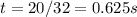
b. The ball land back on the ground when s(t) = 0: