Question

Annabell invested $2000 into an account earning 3.5% interest compounded continuously. How long will it take to double her investment?

Answer 1

`\$2000` will become
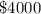`\$4000` in 19.80 years that is approximately 20 years when compounded continuously at the annual interest rate of
`3.5\%`

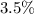
Solution:

Given that

Amount investe by Annabell =
`\$2000`,

Rate if interest
`= 3.5\% = 0.035`

`Required \ amount = double \ of \ investment = 2* \$2000 = \$4000`

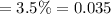
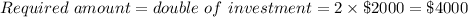
And most important thing that interest is compounded continuously . Formula of Amount where interest is compounded continuously is as follows ,

`\mathrm{A}=\mathrm{P} e^{\mathrm{r}{t}}`

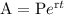
Where A is final amount,

P is principal Amount,

r = rate of interest

And t = duration in years

In our case
`A = \$4000; \ P = \$2000; \ r = 0.035`

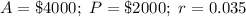
Need to evaluate t that is number of year.

On substituting given values in formula of amount we get

`\begin{array}{l}{4000=2000 e^(0.035 t)} \\\\ {=>(4000)/(2000)=e^(0.035 t)} \\\\ {\Rightarrow 2=e^(0.035 t)}\end{array}`

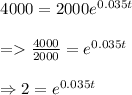
Taking log both the sides,

`\ln (2)=0.035 \mathrm{t} * \ln (\mathrm{e})`

`\Rightarrow \mathrm{t}=(\ln (2))/(0.035)==19.80`

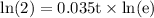
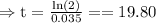
That is approximately 20 years.