Question

A planet or butting a distant star has been observed to have an orbital period of 0.76 earth years at a distance of 1.2 au. What is the mass of the star the planet is orbiting

Answer 1

0.3 is correct for E2020

Step-by-step explanation:

Answer 2

The mass of the star is, M = 5.9567x10³⁰ Kg

Step-by-step explanation:

Given

The orbital period of the planet, T = 0.76 year

= 2.3967x10⁷ seconds

The distance between planet and sun, R+h = 1.2 a.u

= 1.795 x 10¹¹ meters

The orbital period of the planet is given by the formula

`T={2\pi\sqrt{((R+h)^(2))/(GM)}}`

Squaring and solving for M

`M=(4\pi ^(2) (R+h)^(3))/(GT^(2) )`

Substituting the given values in the above equation

`M=(4\pi ^(2)(1.795X10^(11) )^(3) )/(6.673X10^(-11)X(2.3967X10^(7))^(2))`

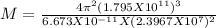
M = 5.9567 x 10³⁰ Kg

Hence, the mass of the star the planet is orbiting, M = 5.9567 x 10³⁰ Kg