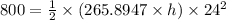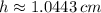Question

You are designing a rotating metal flywheel that will be used to store energy. The flywheel is to be a uniform disk with radius 27.0 cm . Starting from rest at t = 0, the flywheel rotates with constant angular acceleration 3.00 rad/s2 about an axis perpendicular to the flywheel at its center If the flywheel has a density (mass per unit volume) of 8600 kg/m3, what thickness must it have to store 800 J of kinetic energy at t = 8.00 s?

Answer 1

`h\approx1.0443\,cm`

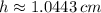
Step-by-step explanation:

Given:

• Radius of flywheel,
  `r= 27 \, cm`

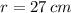
• initial time,
  `t_i=0\,s`

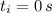
• Angular acceleration of flywheel,
  `\alpha=3\,rad.s^(-1)`

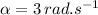
• Density of flywheel,
  `\rho=8600\,kg.m^(-3)`

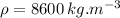
• kinetic energy after final time,
  `KE=800\, J`

• Final time,
  `t_f=8\,s`

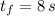
We know for rotational kinetic energy:

`KE=(1)/(2) I.\omega^2`.................................(1)

where:

I = mass moment of inertia for the given mass geometry

`\omega`= angular velocity in radians per second,

Here,

`I= (1)/(2) M.r^2`

∵
`mass=density* volume`

`I= (1)/(2) * (8600* \pi* 0.27^2* h)* 0.27`

`I=265.8947* h`

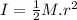
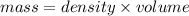
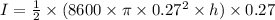
Now,

`\omega= \alpha* t_f`

`\omega=3*8`

`\omega=24 \,rad.s^(-1)`

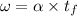
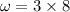
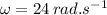
∴Using eq. (1)

`800=(1)/(2) * (265.8947* h)* 24^2`

`h\approx1.0443\,cm`