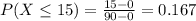Question

Suppose the probability of producing a defective light bulb from a production line is the same over an interval of 90 minutes. Which of the following distributions would you use to determine the probability that a defective light bulb will be produced in a 15-minute interval? A) Normal distribution B) Poisson distribution C) Uniform distribution D) Exponential distribution

Answer 1

C) Uniform distribution

Explanation:

An uniform probability is a case of probability in which each outcome is equally as likely. In this case, the probability of producing a defective light bulb from a production line is the same over an interval of 90 minutes, so the correct answer is C.

We can calculate the probability.

Uniform probability distribution

For this situation, we have a lower limit of the distribution that we call a and an upper limit that we call b.

The probability that we find a value X lower than x is given by the following formula.

`P(X \leq x) = (x - a)/(b-a)`

For this problem, we have that:

Uniformily distributed over a 90 minute interval, that is, between 0 and 90, so
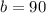`b = 90` and
`a = 0`.

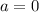We want to find
`P(X \leq 15) = (15-0)/(90-0) = 0.167`