Question

Consider functions of the form f(x)=a^x for various values of a. In particular, choose a sequence of values of a that converges to e. (like a=1, a=1.5, a=2, a=2.5, a=2.6, a=2.7...a=3). Grpah f(x), f'(x), and the line tangent to f(x) for x=2 for each of your values of a. Describe the relationship between f and its derivatives as the values of the parameter a pass through e.

Answer 1

A. As "a"⇒e, the function f(x)=aˣ tends to be its derivative.

Explanation:

A. To show the stretched relation between the fact that "a"⇒e and the derivatives of the function, let´s differentiate f(x) without a value for "a" (leaving it as a constant):

`f(x)=a^(x)\\ f'(x)=a^xln(a)`

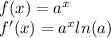
The process will help us to understand what is happening, at first we rewrite the function:

`f(x)=a^x\\ f(x)=e^(ln(a^x))\\ f(x)=e^(xln(a))\\`

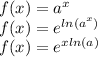
And then, we use the chain rule to differentiate:

`f'(x)=e^(xln(a))ln(a)\\ f'(x)=a^xln(a)`

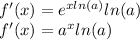
Notice the only difference between f(x) and its derivative is the new factor ln(a). But we know that ln(e)=1, this tell us that as "a"⇒e, ln(a)⇒1 (because ln(x) is a continuous function in (0,∞) ) and as a consequence f'(x)⇒f(x).

In the graph that is attached it´s shown that the functions follows this inequality (the segmented lines are the derivatives):

if a<e<b, then aˣln(a) < aˣ < eˣ < bˣ < bˣln(b) (and below we explain why this happen)

Considering that ln(a) is a growing function and ln(e)=1, we have:

if a<e<b, then ln(a)< 1 <ln(b)

if a<e, then aˣln(a)<aˣ

if e<b, then bˣ<bˣln(b)

And because eˣ is defined to be the same as its derivative, the cases above results in the following

if a<e<b, then aˣ < eˣ < bˣ (because this function is also a growing function as "a" and "b" gets closer to e)

if a<e, then aˣln(a)<aˣ<eˣ ( f'(x)<f(x) )

if e<b, then eˣ<bˣ<bˣln(b) ( f(x)<f'(x) )

but as "a"⇒e, the difference between f(x) and f'(x) begin to decrease until it gets zero (when a=e)