Question

An oil refinery is located on the north bank of a straight river that is 3km wide. A pipeline is to be constructed from the refinery to storage tanks located on the south bank of the river 8km east of the refinery. The cost of laying pipe is $500,000/km over land to point P on the north bank and $1,000,000/km under river to the tanks. What is the minimal cost to construct a pipeline from the refinery to the storage tanks?

Answer 1

$6,598,076.21

Step-by-step explanation:

THE KEY IS TO FIND OUT THE COST FUNCTION, the calculations are very easy!!!

In order to find the cost function, take a look at the drawing attached.

We can see the river (sort of) that is 3 km wide and the storage tanks on the other side of the river 8 km apart.

Laying pipes under (across) the river costs 1,000,000 the km & laying pipes over land costs 500,000 per km.

So basically the cost function is 1,000,000 multiplied by something plus 500,000 multiplied by another something.

The distance across the river can be found by using Pythagoras Theorem. A side is 3 km the other is unknown, so we call it X. And it is equal to:

`\sqrt{3^(2) +x^(2)}=\\\sqrt{9 +x^(2)}`

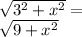
And we multiply it by 1,000,000; the cost of laying pipe under the river, the we get:

`1000000\sqrt{9+x^(2)`

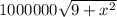
The distance over the land is (8-x), as we can see in the drawing. So we multiply it by its cost, 500,000. And we get 500,000(8-x).

So the cost function f(x) would be:

`f(x)=1000000\sqrt{9+x^(2)} + 500000(8-x)`

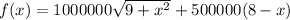
From here, we just have to differentiate and the derivative found must be equal to zero in order to minimize cost.

The value of x when the derivative is zero is plugged in the original function to get the cost.

LET'S DO THIS

`f(x)=1000000\sqrt{9+x^(2)} + 500000(8-x)\\f(x)=1000000(9+x^(2))^(1/2)+4000000-500000x\\f'(x)=(1)/(2) 1000000(9+x^(2))^(-1/2)(2x)-500000\\\\f'(x)=(1000000x)/(√(9+x^2))  - 500000`

f'(x)=0

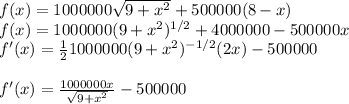
`f'(x)=(1000000x)/(√(9+x^2))  - 500000=0\\(1000000x)/(√(9+x^2))  = 500000\\(2x)/(√(9+x^2))  = 1\\2x={√(9+x^2)}\\4x^2=9+x^2\\3x^2=9\\x^2=3\\x=√(3) \\`

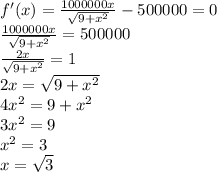
And we plug square root of 3 in the original cost function ad we get

`f(√(3) )=1000000\sqrt{9+x^(2)} + 500000(8-x)\\f(√(3))=1000000\sqrt{9+(√(3) )^(2)} + 500000(8-(√(3)))\\f(√(3))=1000000√(9+3) + 500000(8-(√(3)))\\f(√(3))=1000000√(12)+500000(6.27)\\f(√(3))=1000000(3.46)+500000(6.27)\\f(√(3))=3464101.62+3133974.60\\f(√(3))=6598076.21\\`

so the minimal cost is $6,598,076.21