Question

An equilibrium mixture of PCl₅(g), PCl₃(g), and Cl₂(g) has partial pressures of 217.0 Torr, 13.2 Torr, and 13.2 Torr, respectively. A quantity of Cl₂(g) is injected into the mixture, and the total pressure jumps to 263.0 Torr. The appropriate chemical equation is PCl₃(g)+Cl₂(g)↽−−⇀PCl₅(g) Calculate the new partial pressures after equilibrium is reestablished.

Answer 1

PCl₅ = 223.4 torr

PCl₃ = 6.8 torr

Cl₂ = 26.4 torr

Step-by-step explanation:

For gas substances, the equilibrium constant can be calcultaed based on the partial pressures (Kp). For a generic reaction:

aA(g) + bB(g) ⇄ cC(g) + dD(g)

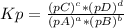`Kp = ((pC)^c*(pD)^d)/((pA)^a*(pB)^b)`, where pX is the partial pressure of X.

The reaction with the gas mixture given is:

PCl₅(g) ⇄ PCl₃(g) + Cl₂(g)

Kp = [(pPCl₃)*(pCl₂)]/(pPCl₅)

Kp = [13.2*13.2]/217

Kp = 0.803

When more Cl₂ is added, for Le Chatêlier's principle, the equilibrium will shift for the left, more PCl₅ will be formed, and the equilibrium will be reestablished.

The initial total pressure was 243.4 torr, so if it jumps to 263.0 torr, it was added 19.6 torr of Cl₂, so the partial pressure of Cl₂ is 32.8 torr. For the reaction:

PCl₅(g) ⇄ PCl₃(g) + Cl₂(g)

217.0 13.2 32.8 Initial

+x -x -x Reacts (stoichiometry is 1:1:1)

217 + x 13.2-x 32.8-x Equilibrium

So, the equilibrium constant must be:

`Kp = ((13.2-x)*(32.8-x))/(217+x)`

0.803 = (432.96 - 46x + x²)/(217 + x)

432.96 - 46x + x² = 174.251 + 0.803x

x² - 46.803x + 258.71 = 0

By Bhaskara's equation:

Δ = (46.803)² - 4*1*258.71

Δ = 1,155.68

x =[-(- 46.803) ±√1,155.68]/2

x' = (46.803 + 33.99)/2

x' = 40.40

x'' = (46.803 - 33.99)/2

x'' = 6.40

x < 32.8, so x = 6.40

The new partial pressures are:

PCl₅ = 217.0 + 6.40 = 223.4 torr

PCl₃ = 13.2 - 6.40 = 6.8 torr

Cl₂ = 32.8 - 6.40 = 26.4 torr