The base and height of the triangle whose area is 51
 and base of a triangle is twelve more than twice its height are 21.49 cm and 4.745 cm respectively.
and base of a triangle is twelve more than twice its height are 21.49 cm and 4.745 cm respectively.
Solution:
Given that
The base of a triangle is twelve more than twice its height
And area of triangle = 51 square centimeter
Let’s assume height of triangle = "x" cm
So base of triangle = 12 + (2
 height ) = 2x + 12
height ) = 2x + 12

On substituting the given value of area and assumed values of height and base in above formula we get
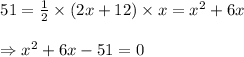
We can find solution of this equation using quadratic formula.
According to quadratic formula for general equation
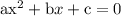 solution of the equation is given by
solution of the equation is given by
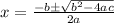
Our equation is
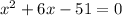
So in our case, a = 1 , b = 6 and c = -51
On applying quadratic formula we get
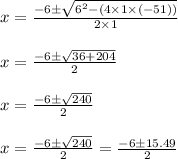
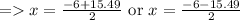
As dimensions of triangle cannot be negative so neglect negative value

Height of triangle = x = 4.745 cm
Base of triangle = 12 + ( 2 x 4.745 ) = 12 + 9.49 = 21.49 cm
Hence base and height of the triangle whose area is 51
 and base of a triangle is twelve more than twice its height are 21.49 cm and 4.745 cm respectively.
and base of a triangle is twelve more than twice its height are 21.49 cm and 4.745 cm respectively.