Question

The base of a triangle is twelve more than twice its height. If the area of the triangle is 51 square​ centimeters, find its base and height.

Answer 1

The base and height of the triangle whose area is 51
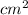`cm^2` and base of a triangle is twelve more than twice its height are 21.49 cm and 4.745 cm respectively.

Solution:

Given that

The base of a triangle is twelve more than twice its height

And area of triangle = 51 square centimeter

Let’s assume height of triangle = "x" cm

So base of triangle = 12 + (2
`*` height ) = 2x + 12

`\text { Area of triangle }=(1)/(2) * \text { Base } * \text { height }`

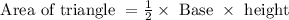
On substituting the given value of area and assumed values of height and base in above formula we get

`\begin{array}{l}{51=(1)/(2) *(2 x+12) * x=x^(2)+6 x} \\\\ {\Rightarrow x^(2)+6 x-51=0}\end{array}`

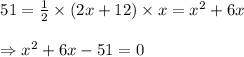
We can find solution of this equation using quadratic formula.

According to quadratic formula for general equation
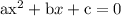`\mathrm{ax}^(2)+\mathrm{b} x+\mathrm{c}=0` solution of the equation is given by

`x=\frac{-b \pm \sqrt{b^(2)-4 a c}}{2 a}`

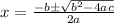
Our equation is
`x^(2)+6 x-51=0`

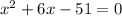
So in our case, a = 1 , b = 6 and c = -51

On applying quadratic formula we get

`\begin{array}{l}{x=\frac{-6 \pm \sqrt{6^(2)-(4 * 1 *(-51))}}{2 * 1}} \\\\ {x=(-6 \pm √(36+204))/(2)} \\\\ {x=(-6 \pm √(240))/(2)} \\\\ {x=(-6 \pm √(240))/(2)=(-6 \pm 15.49)/(2)}\end{array}`

`=>x=(-6+15.49)/(2) \text { or } x=(-6-15.49)/(2)`

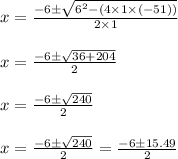
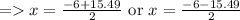
As dimensions of triangle cannot be negative so neglect negative value

`x=(-6+15.49)/(2)=(9.49)/(2)=4.745`

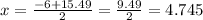
Height of triangle = x = 4.745 cm

Base of triangle = 12 + ( 2 x 4.745 ) = 12 + 9.49 = 21.49 cm

Hence base and height of the triangle whose area is 51
`cm^2` and base of a triangle is twelve more than twice its height are 21.49 cm and 4.745 cm respectively.