Question

A 12.0-g bullet is fired horizontally into a 104-g wooden block that is initially at rest on a frictionless horizontal surface and connected to a spring having spring constant 154 N/m. The bullet becomes embedded in the block. If the bullet-block system compresses the spring by a maximum of 83.0 cm, what was the speed of the bullet at impact with the block?

Answer 1

v₀ = 292.3 m / s

Step-by-step explanation:

Let's analyze the situation, on the one hand we have the shock between the bullet and the block that we can work with at the moment and another part where the assembly (bullet + block) compresses a spring, which we can work with mechanical energy, as the data they give us are Let's start with this second part.

We write the mechanical energy when the shock has passed the bodies

Em₀ = K = ½ (m + M) v²

We write the mechanical energy when the spring is in maximum compression

`Em_(f)` =
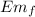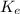`K_(e)` = ½ k x²

Em₀ =
`Em_(f)`

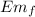
½ (m + M) v² = ½ k x²

Let's calculate the system speed

v = √ [k x² / (m + M)]

v = √[154 0.83² / (0.012 +0.104) ]

v = 30.24 m / s

This is the speed of the bullet + Block system

Now let's use the moment to solve the shock

Before the crash

p₀ = m v₀

After the crash

`p_(f)` = (m + M) v

The system is formed by the bullet and block assembly, so the forces during the crash are internal and the moment is preserved

p₀ =
`p_(f)`

m v₀ = (m + M) v

v₀ = v (m + M) / m

let's calculate

v₀ = 30.24 (0.012 +0.104) /0.012

v₀ = 292.3 m / s