Answer:
v=3.649 m/s
Step-by-step explanation:
Lets start with the force of gravity on the elevator.
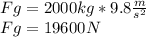
But the friction clamp opposes this with a force of 17000 N
So the Net force on the elevator is
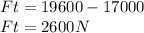
Kinetic Energy
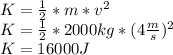
The motion will be describe
original Kinetic energy + work done = final kinetic energy + spring energy
