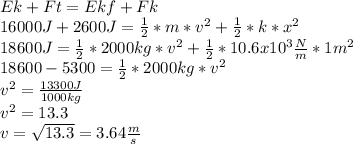Question

In a "worst-case" design scenario, a 2000 kg elevator with broken cables is falling at 4.00 m/s when it first contacts a cushioning spring at the bottom of the shaft. The spring is supposed to stop the elevator, compressing 2.00 m as it does so. Spring coefficient is 10.6 kN/m. During the motion a safety clamp applies a constant 17000-N frictional force to the elevator.What is the speed of the elevator after it has moved downward 1.00 m from the point where it first contacts a spring?

Answer 1

v=3.649 m/s

Step-by-step explanation:

Lets start with the force of gravity on the elevator.

`Fg=2000 kg* 9.8(m)/(s^(2) )  \\Fg= 19600N`

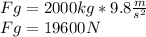
But the friction clamp opposes this with a force of 17000 N

So the Net force on the elevator is

`Ft=19600 - 17000 \\Ft= 2600 N`

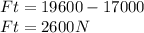
Kinetic Energy

`K=(1)/(2)*m*v^(2)\\K=(1)/(2)*2000kg*(4(m)/(s)) ^(2)\\K=16000J`

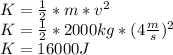
The motion will be describe

original Kinetic energy + work done = final kinetic energy + spring energy

`Ek+Ft=Ekf+Fk\\16000J+2600J=(1)/(2)*m*v^(2)+(1)/(2)*k*x^(2) \\18600J=(1)/(2)*2000kg*v^(2)+ (1)/(2)*10.6x10^(3)(N)/(m) *1m^(2)\\18600-5300=(1)/(2)*2000kg*v^(2)\\v^(2)=(13300J)/(1000kg)\\v^(2)=13.3\\v=√(13.3)=3.64 (m)/(s)`