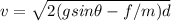Question

A block of mass mm starts from rest and slides down from the top of a wedge of height hh and length dd. The surface of the wedge forms an angle of \thetaθ with respect to the horizontal direction. The force of kinetic friction between the block and the wedge is \vec{f} f ​ . How fast is the block traveling when it reaches the bottom of the wedge?

Answer 1

`v=√( 2 (g sin\theta- f/m) d)`

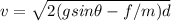
Step-by-step explanation:

Given that

Mass = m

Height = h

Length = d

Angle = θ

Friction force = f

When block slides downward then friction force will act upwards

The force due to gravity along inline plane

Fg= mg sinθ

Lets 'a' is the acceleration

From Newtons law

mg sinθ - f = m a

a= (g sinθ - f/m)

Given that initial speed u= o ,lets v is final speed

v²=u²+ 2 a s

v²=2 x (g sinθ - f/m) x d

`v=√( 2 (g sin\theta- f/m) d)`