Question

In a fast-pitch softball game the pitcher is impressive to watch, as she delivers a pitch by rapidly whirling her arm around so that the ball in her hand moves in a circle. In one instance, the radius of the circle is 0.681 m. At one point on this circle, the ball has an angular acceleration of 67.7 rad/s^2 and an angular speed of 18.6 rad/s. (a) Find the magnitude of the total acceleration (centripetal plus tangential) of the ball. (b) Determine the angle of the total acceleration relative to the radial direction.

Answer 1

(a). The magnitude of the total acceleration of the ball is 239.97 m/s².

(b). The angle of the total acceleration relative to the radial direction is 11.0°

Step-by-step explanation:

Given that,

Radius of the circle = 0.681 m

Angular acceleration = 67.7 rad/s²

Angular speed =18.6 rad/s

We need to calculate the centripetal acceleration of the ball

Using formula of centripetal acceleration

`a_(c)=\omega^2* r`

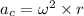
Put the value into the formula

`a_(c)=(18.6)^2*0.681`

`a_(c)=235.5\ m/s^2`

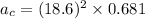
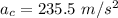
We need to calculate the tangential acceleration of the ball

Using formula of tangential acceleration

`a_(t)=r\alpha`

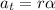
Put the value into the formula

`a_(t)=0.681*67.7`

`a_(t)=46.104\ m/s^2`

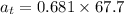
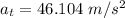
(a). We need to calculate the magnitude of the total acceleration of the ball

Using formula of total acceleration

`a=\sqrt{a_(c)^2+a_(t)^2}`

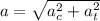
Put the value into the formula

`a=√((235.5)^2+(46.104)^2)`

`a=239.97\ m/s^2`

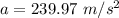
(b). We need to calculate the angle of the total acceleration relative to the radial direction

Using formula of the direction

`\theat=\tan^(-1)((a_(t))/(a_(c)))`

Put the value into the formula

`\theta=\tan^(-1)((46.104)/(235.5))`

`\theta=11.0^(\circ)`

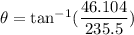
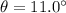
Hence, (a). The magnitude of the total acceleration of the ball is 239.97 m/s².

(b). The angle of the total acceleration relative to the radial direction is 11.0°