Answer:
The bucket's velocity is

Explanation:
Given
Height above the ground, H = 12 m
Mass of bucket, m = 0.5 kg
Height of bucket, h = 4m
Taking acceleration of gravity, g as 9.8m/s²
First, we calculate the potential energy when bucket is on scaffolding (just about to fall) its total energy is 100%
P.E = mgH
P.E = 0.5 * 9.8 * 12
P.E = 58.8 J
At this point, the object is at rest, so the kinetic energy is 0 J
When the object is at 4 m above the ground, the bucket's total mechanical energy is as follows using conservation of energy
M.E
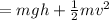
Where Total mechanical energy (M.E) = P.E (calculated above) = 58.8 J
By substitution, we have
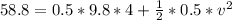
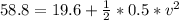

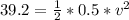

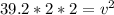
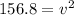 --- Take Square roots
--- Take Square roots
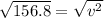
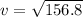
 ---- Approximated
---- Approximated
Hence, the bucket's velocity is
