Question

Suppose the demand for newspapers is equally likely to be any integer between 0 and 24, i.e., X ~ Unif{0,1,2,…,24} and we buy them in the morning for $.30, we sell them for $1, and we get $.10 for any newspapers leftover at the end of the day from the recycling company. How many newspapers should we obtain to sell during the day?

Answer 1

We should obtain 19 newspapers to maximize the expected profits.

Step-by-step explanation:

In this problem we have to optimize the quantity of newspaper we buy to maximize the profit.

We can divide the analysis in two parts:

1) If the amount of newspaper sold (S) is more than the newspaper we bougth (B), the profit is
`G_1=(1.0-0.3)*B=0.7*B`.

This occurs with probability
`P(S>B)=1-B/24`, as S is uniformly distributed.

2) If the amount of newspaper sold (S) is less than the newspaper we bougth (B) we have a profit of:

`G_2=1.0*S+0.1*(B-S)-0.3*B=0.9S-0.2B`

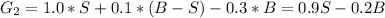
This happens with a probability of
`P(S≤B)=B/24`.

As we have S in our profit equation, we have to calculate the expected value of S to estimate the profit in function of B.

If S is smaller than B, then it is uniformly distributed between 0 and B. The expected value can be calculated as:

`E[S]=(B-0)/(2) =B/2`

Then, the expected profit formula for S<B is
`G_2=0.9S-0.2B=0.45B-0.2B=0.25B`

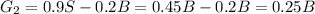
The total profit tcan be calculated by adding the two parts analized previously: when S>B and when S<B, affected by the probability of occurrence:

`G=P(S>B)*G_1+P(S\leq B)*G_2\\\\G=(1-(B)/(24))*(0.7B)+((B)/(24) )*0.25B\\\\G=0.7B-(0.7)/(24)B^2+(0.25)/(24)B^2\\\\G=-0.01875B^2+0.7B`

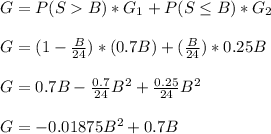
To maximize the profit G, we derive and equal zero

`(dG)/(dB)= -0.01875*2*B+0.7=0\\\\-0.0375B+0.7=0\\\\B=0.7/0.0375=18.66 \approx 19`

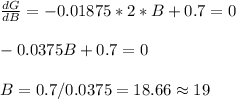
We should obtain 19 newspapers to maximize the expected profits.