Answer:
The populaton in year 1991 will be of 5178.9 million of people
and the population in year 2020 will be of 8524.60 million of people
Explanation:
We measure the time t in years and let t=0 in the year 1950.
We measure the population P(t) in millions of people, then P(0)=2560 and P(10) = 3040.
Since we are assuming that dp/dt=kP, this theorem gives the following.
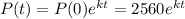
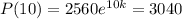

The relative growth rate is about 1.7% per year and the model is
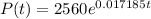
Year 1991 is equal in our formula to 41 and year 2020 is equal to 70. Replacing,
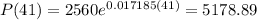
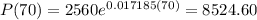
Therefore the populaton in year 1991 will be of 5178.9 million of people and the population in year 2020 will be of 8524.60 million of people