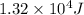Answer : The correct option is, (a)
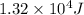
Solution :
The conversions involved in this process are :
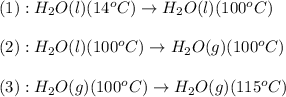
Now we have to calculate the enthalpy change.
![\Delta H=[m* c_(p,l)* (T_(final)-T_(initial))]+n* \Delta H_(vap)+[m* c_(p,g)* (T_(final)-T_(initial))]](https://img.qammunity.org/2020/formulas/chemistry/college/xnc35f6zzup0skxjx3kg1pr34173rvvui1.png)
where,
 = enthalpy change or heat required = ?
= enthalpy change or heat required = ?
m = mass of water = 5.00 g
 = specific heat of liquid water =
= specific heat of liquid water =
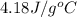
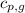 = specific heat of liquid water =
= specific heat of liquid water =
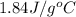
n = number of moles of water =
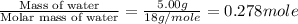
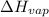 = enthalpy change for vaporization = 40.67 KJ/mole = 40670 J/mole
= enthalpy change for vaporization = 40.67 KJ/mole = 40670 J/mole
Now put all the given values in the above expression, we get
![\Delta H=[5.00g* 4.18J/g^oC* (100-14)^oC]+0.278mole* 40670J/mole+[5.00g* 1.84J/g^oC* (115-100)^oC]](https://img.qammunity.org/2020/formulas/chemistry/college/10iy29kzdvi6n8m4kcsadmtr4g9hmkgift.png)
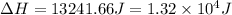
Therefore, the enthalpy change is,