Question

A 2.36 kg block resting on a frictionless surface is attached to an ideal spring with spring constant k = 260 Nm . A force is applied to the block which changes its position from xi=5.89 cm to xf=−15.4 cm , each distance measured relative to the equilibrium position of the block. While the block is being moved, find

(a) the work done by the spring and
(b) the work done by the applied force.

Answer 1

-2.63 Joules

2.63 Joules

Step-by-step explanation:

`x_i` = Initial compression = 5.89 cm

`x_f` = Final compression = -15.4 cm

k = Spring constant = 260 Nm

Work done by a spring is given by

`W=(1)/(2)k(x_i^2-x_f^2)\\\Rightarrow W=(1)/(2)260* (0.0589^2-0.154^2)\\\Rightarrow W=-2.63\ J`

Work done by the spring is -2.63 Joules.

Change in kinetic energy is given by

`\Delta K=W_a+W_s`

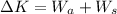
Here, it is assumed that change in kinetic energy is zero as velocity and amlitude are not mentioned.

So,

`0=W_a+W_s\\\Rightarrow W_a=-W_s\\\Rightarrow W_a=--2.63\\\Rightarrow W_a=2.63\ J`

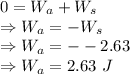
The work done by the applied force is 2.63 Joules.