The expected value of game is $

Solution:
Given, You toss 4 coins and if you toss all heads you win $9.
When you toss anything other than 4 heads you lose $1
We have to find what is the Expected Value of the game?
The expected value is given as:

since we toss 4 coins, total outcomes
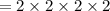
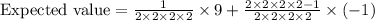
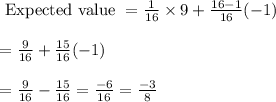
Hence, the expected value is
