Question

Which system of linear inequalities is graphed?

A. y < 3x-2
x + 2y ≥ 4

B. y < 3x - 2
x + 2y > 4

C. y > 3x - 2
x + 2y < 4

D. y ≥ 3x - 2
x + 2y ≤ 4

Answer 1

D.
`y\geq 3x - 2\\x + 2y\leq 4`

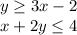
Explanation:

From the graph, we can conclude that,

1. The two lines are continuous lines and not broken lines. So, the inequality sign should be either
`\geq \textrm{ or }\leq`.

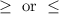2. The points on the lines of the shaded region are also included in the solution.

The only option that matches with the above conditions is option D. So, option D is the correct answer.

Let us verify it.

Now, let us consider a point that is inside the shaded region and also on any one line. Let us take
`(0,2)`.

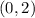Plug in 0 for x and 2 for y in each of the options and check which inequality holds true.

Option A:

`y < 3x-2\\ 2 < 3(0)-2\\2<-2\\\\x + 2y \geq  4\\0+2(2)\geq 4\\4\geq 4`

So, inequality 1 is wrong as -2 is less than 2.

Option B:

`y < 3x - 2\\ 2<3(0)-2\\2<-2\\\\x + 2y > 4\\0+2(2)>4\\4>4`

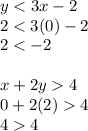
Both the inequalities are wrong.

Option C:

`y > 3x - 2\\2>3(0)-2\\2>-2\\\\x + 2y < 4\\0+2(2)<4\\4<4`

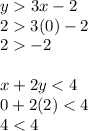
Inequality 2 is wrong.

Option D:

`y\geq 3x - 2\\2\geq 3(0)-2\\2\geq -2\\\\x + 2y\leq 4\\0+2(2)\leq 4\\4\leq 4`

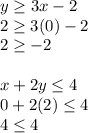
Here, both inequalities are correct.

So, option D is the correct answer.