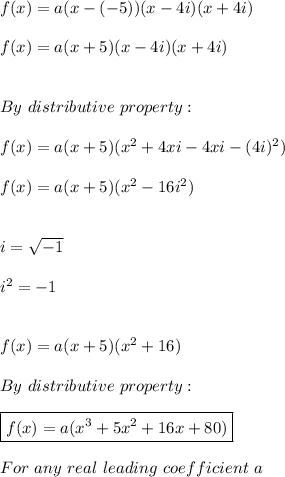Question

Polynomial function that has the zeros -5 and 4i

Answer 1

The polynomial function is:

`\boxed{f(x)=a(x^3+5x^2+16x+80)}`

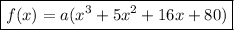
Step-by-step explanation:

In this exercise, we will use two important theorems:

• Fundamental Theorem of Algebra: We can factor completely any polynomial with real number coefficients over the field of complex numbers.

• Complex Conjugate Root Theorem: If a polynomial in one variable has real coefficients, and
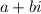  `a+bi` is a root of that polynomial being
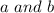  `a \ and \ b` real numbers, then its complex conjugate
  `a-bi` is also a root of the polynomial function.

In this case we have the following roots:

`x_(1)=-5 \ and \ x=4i`

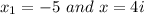
According to the Complex Conjugate Root Theorem:

`x_(3)=-4i \\ \\ Is \ also \ a \ root \ of \ the \ polynomial \ function`

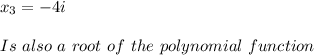
Hence, we can write the function as:

`f(x)=a(x-(-5))(x-4i)(x+4i) \\ \\ f(x)=a(x+5)(x-4i)(x+4i) \\ \\ \\ By \ distributive \ property: \\ \\ f(x)=a(x+5)(x^2+4xi-4xi-(4i)^2) \\ \\ f(x)=a(x+5)(x^2-16i^2) \\ \\ \\ i=√(-1) \\ \\  i^2=-1 \\ \\ \\ f(x)=a(x+5)(x^2+16) \\ \\ By \ distributive \ property: \\ \\ \boxed{f(x)=a(x^3+5x^2+16x+80)} \\ \\ For \ any \ real \ leading \ coefficient \ a`