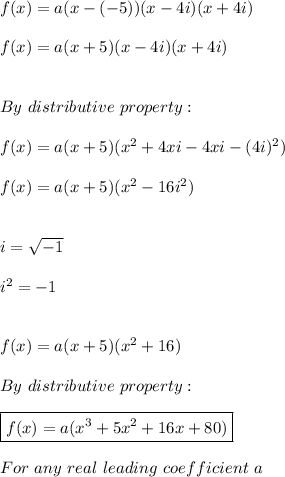The polynomial function is:
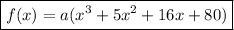
Step-by-step explanation:
In this exercise, we will use two important theorems:
- Fundamental Theorem of Algebra: We can factor completely any polynomial with real number coefficients over the field of complex numbers.
- Complex Conjugate Root Theorem: If a polynomial in one variable has real coefficients, and
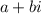 is a root of that polynomial being
is a root of that polynomial being
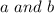 real numbers, then its complex conjugate
real numbers, then its complex conjugate
 is also a root of the polynomial function.
is also a root of the polynomial function.
In this case we have the following roots:
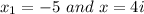
According to the Complex Conjugate Root Theorem:
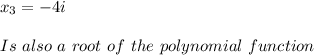
Hence, we can write the function as: