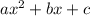Question

Polynomial function that has the zeros -5 and 4i

Answer 1

`P(x) = x^(2)  + x(5-4i) - 20i` is the required polynomial function of the form
`ax^(2)  + bx +c`

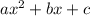
Explanation:

The given zeroes of the polynomial is -5 and 4i.

It implies, the roots of the polynomial is (x+5) and (x-4i)

Now, The Polynomial = Product of all its roots

So, here P(x) = ( x + 5)( x - 4i)

or,
`P(x) = x (x-4i) + 5(x-4i)  = x^(2)  - 4ix + 5x - 20i`

⇒
`P(x) = x^(2)  + x(5-4i) - 20i`

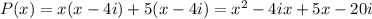
Hence, P(x) is the required polynomial function of the form
`ax^(2)  + bx +c`