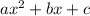Answer:
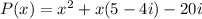 is the required polynomial function of the form
is the required polynomial function of the form
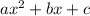
Explanation:
The given zeroes of the polynomial is -5 and 4i.
It implies, the roots of the polynomial is (x+5) and (x-4i)
Now, The Polynomial = Product of all its roots
So, here P(x) = ( x + 5)( x - 4i)
or,
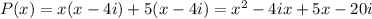
⇒
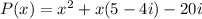
Hence, P(x) is the required polynomial function of the form