Answer:
(2,2) and (3,1)
Explanation:
Since we're given the value of y in the second equation, we can replace the y on the left side of the first equation with 4-x, giving us
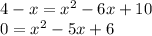
We can factor the expression on the right to get us
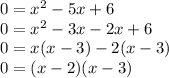
Solving
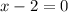 and
and
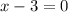 gets us the solutions
gets us the solutions
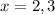 , which we can plug into the second equation to get us
, which we can plug into the second equation to get us
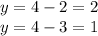
So, our solution set is the pair of points (2,2) and (3,1)