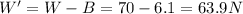Question

A metal block of density 9000kgcm3 weighs 70N in air. Find its weight when it is immersed in paraffin wax of density 800kgm3? (take g=10ms-2)​

Answer 1

63.788 N

Step-by-step explanation:

Density of a metal block = 9000 ×〖10〗^(-6) kgm^(-3)

Mass of the metal block = 70/10 = 7 kg

Volume = Mass/ Density

Volume of the metal block = 7/9000 ×(10)^(-6) kgm^(-3)

= 777.777 m^3

When it’s immersed in water up thrust is acted on a metal block then the weight is reduced due to up thrust, Let’s take W as a New measurement,

W + U = 70

W = 70-U

W = 70 -Vρ_l g

W= 70 – 777.77×800×(10)^(-6)×10

W = 63.778 N

Answer 2

Note: the text says that the density of the block is
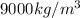`9000 kg/m^3` (not
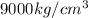`9000 kg/cm^3`, which not a plausible value)

Answer:

63.9 N

Step-by-step explanation:

We want to find the apparent weight of the block when it is in water.

First of all, we know its true weight:

W = 70 N

So we can find the mass of the block:

`m=(W)/(g)=(70)/(10)=7.0 kg`

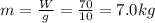
where
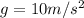`g=10 m/s^2` is the acceleration of gravity.

From the mass and the density, which is

`\rho=9000 kg/m^3`

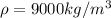
we find the volume of the block:

`V=(m)/(\rho)=(7.0)/(9000)=7.8\cdot 10^(-4) m^3`

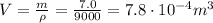
We know that when the block is immersed in paraffin, it is acted upon the buoyant force, which acts upward, and whose magnitude is

`B=\rho_p V g`

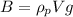
where

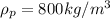`\rho_p = 800 kg/m^3` is the density of paraffin

V is the volume of paraffin displaced, which corresponds to the volume of the block

`g=10 m/s^2`

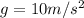
Substituting,

`B=(800)(7.8\cdot 10^(-4))(10)=6.2 N`

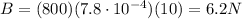
Therefore, the apparent weight of the block in paraffin will be:

`W'=W-B=70-6.1=63.9 N`