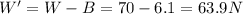Note: the text says that the density of the block is
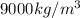 (not
(not
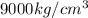 , which not a plausible value)
, which not a plausible value)
Answer:
63.9 N
Step-by-step explanation:
We want to find the apparent weight of the block when it is in water.
First of all, we know its true weight:
W = 70 N
So we can find the mass of the block:
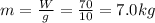
where
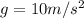 is the acceleration of gravity.
is the acceleration of gravity.
From the mass and the density, which is
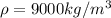
we find the volume of the block:
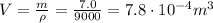
We know that when the block is immersed in paraffin, it is acted upon the buoyant force, which acts upward, and whose magnitude is
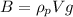
where
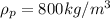 is the density of paraffin
is the density of paraffin
V is the volume of paraffin displaced, which corresponds to the volume of the block
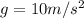
Substituting,
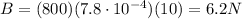
Therefore, the apparent weight of the block in paraffin will be: