Question

Suppose the roots of the equation 2x^2−5x−6=0 are α and β.Find the quadratic equation with roots 1/α and 1/β.​

Answer 1

The quadratic equation with roots 1/α and 1/β is
`6 x^(2)+5 x-2=0`

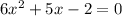
Solution:

Given, roots of equation
`2 x^(2)-5 x-6=0 \text { are } \alpha, \beta`

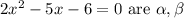
We have to find equation whose roots are 1/α, and 1/β.

We know that,

`\text { sum of roots }=\frac{-x \text { cosficient }}{x^(2) \text { coefficient }} \rightarrow \alpha+\beta=(-(-5))/(2) \rightarrow \alpha+\beta=(5)/(2)`

`\text { And, product of roots }=(c o n s t a n t)/(x^(2) c o e f f i c i e n t) \rightarrow \alpha \beta=(-6)/(2) \rightarrow \alpha \beta=-3`

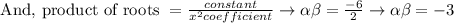
Now, we know that, general form of an equation is

`x^(2)-(\text { sum of roots }) x+\text { product of roots }=0`

Then, equation whose roots 1/α and 1/β is

`\begin{array}{l}{x^(2)-\left((1)/(\alpha)+(1)/(\beta)\right) x+(1)/(\alpha) * (1)/(\beta)=0} \\\\ {\rightarrow x^(2)-\left((\alpha+\beta)/(\alpha \beta)\right) x+(1)/(\alpha \beta)=0}\end{array}`

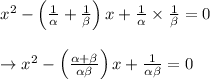
from above given equation,

`\begin{array}{l}{\rightarrow x^(2)-\left(((5)/(2))/(-3)\right) x+(1)/(-3)=0} \\\\ {\text { multiplying equation with }-3} \\\\ {\rightarrow-3 x^(2)-(5)/(2) x+1=0} \\\\ {\text { multiplying equation with } 2} \\\\ {\rightarrow-6 x^(2)-5 x+2=0} \\\\ {\rightarrow-6 x^(2)-5 x+2=0} \\\\ {\text { multiplying equation with }-1} \\\\ {\rightarrow 6 x^(2)+5 x-2=0} \\\\ {\text { Hence, the required line equation is } 6 x^(2)+5 x-2=0}\end{array}`