The quadratic equation with roots 1/α and 1/β is
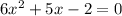
Solution:
Given, roots of equation
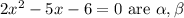
We have to find equation whose roots are 1/α, and 1/β.
We know that,
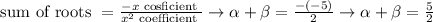
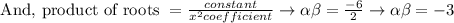
Now, we know that, general form of an equation is
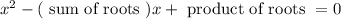
Then, equation whose roots 1/α and 1/β is
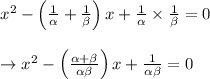
from above given equation,
