Answer:
All positive integers except multiple of 5.
Explanation:
From the rule of divisibility, a number's last digit should be either 0 or 5 for it to be divisible by 5.
For
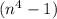 to be a multiple of 5, the last digit of
to be a multiple of 5, the last digit of
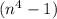 should be 0 or 5. In other words, the last digit of
should be 0 or 5. In other words, the last digit of
 should be 1 or 6.
should be 1 or 6.
The last digit of
 is 1 if
is 1 if
 is an odd number except those that are multiples of 5.
is an odd number except those that are multiples of 5.
The last digit of
 is 6 if
is 6 if
 is an even number except those that are multiples of 5.
is an even number except those that are multiples of 5.
Therefore, the possible values of
 are all positive integers except those that are multiples of 5.
are all positive integers except those that are multiples of 5.