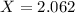Answer:
a) There is a 15.62% probability that a randomly selected two-liter bottle would contain between 1.95 and 2.03 liters.
b) The score is
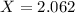
Explanation:
Problems of normally distributed samples can be solved using the z-score formula.
In a set with mean
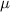 and standard deviation
and standard deviation
 , the zscore of a measure X is given by
, the zscore of a measure X is given by
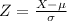
After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X. Subtracting 1 by the pvalue, we This p-value is the probability that the value of the measure is greater than X.
In this problem, we have that
The fill volumes are normally distributed with a mean of 1.97 liters and a variance of 0.04 (liter)2 (i.e. a standard deviation of 0.2 liter). This means that
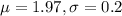 .
.
a. Find the probability that a randomly selected two-liter bottle would contain between 1.95 and 2.03 liters.
This is the pvalue of the Z score of X = 2.03 subtracted by the pvalue of the Z score of X = 1.95.
X = 2.03
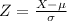
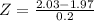
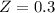
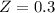 has a pvalue of 0.6179
has a pvalue of 0.6179
X = 1.95
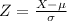
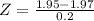
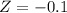
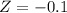 has a pvalue of 0.4617.
has a pvalue of 0.4617.
This means that there is a 0.6179-0.4617 = 0.1562 = 15.62% probability that a randomly selected two-liter bottle would contain between 1.95 and 2.03 liters.
b. If X is the fill volume of a randomly selected two-liter bottle, find the value of x for which P(X > x) = 0.3228.
This is the value of X when Z has a pvalue of 1-0.3228 = 0.6772. This is when
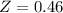 . So:
. So:
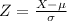
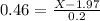
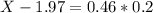
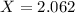
The score is