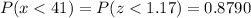Question

Use the normal distribution to approximate the desired probability. A certain question on a test is answered correctly by 25.0 percent of the respondents. Estimate the probability that among the next 140 responses there will be at most 41 correct answers.

Answer 1

The probability that there will be at most 41 correct answers is 0.8790

Explanation:

We can aproximate the probability by using a binomial distribution where:

p: A question on a test is answered correctly

n: number of responses

So, the mean of the distribution is given by:

`\mu= n* p= 140 * 0.25=35`

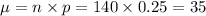
and the standar deviation is given by:

`\sigma=√(n* p* q) =√(n* p* (1-p)) =√(140* 0.25* 0.75) =5.123`

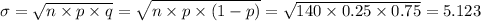
The normalized variable for 41 correct answers is:

`z=(x-\mu)/(\sigma)=(41-35)/(5.123) =1.17`

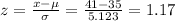
Hence, the probability that there will be at most 41 correct answers is:

`P(x<41)=P(z<1.17)=0.8790`