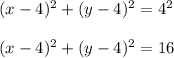Question

NEED HELP QUICK! 30 POINTS!!!

Find an equation of the circle and sketch it: k Center on line y=8–x, tangent to both axes

Answer 1

`(x-4)^2+(y-4)^2=16`

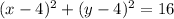
Explanation:

Let A(a,b) be the center of the circle. This point lies on the liny y = 8 - x.

So,

`b=8-a`

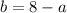
Let points B and C be tangent points, so

`B(a,0)\\ \\C(0,b)=(0,8-a)`

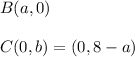
Find the radii AB and AC:

`AB=√((a-a)^2+(8-a-0)^2)=|8-a|\\ \\AC=√((a-0)^2+(8-a-(8-a))^2)=|a|`

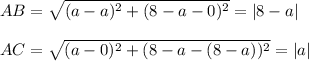
All circle's radii are the same, so

`|8-a|=|a|\\ \\8-a=a\ \text{or}\ 8-a=-a`

Solve each equation:

`\2a=8\\ \\a=4`

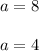
or

`8=0`

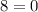
has no solutions.

Thus, the center of the circle is at point (4,4) and the radius is r = |a| = 4.

Therefore, the equation of the circle is

`(x-4)^2+(y-4)^2=4^2\\ \\(x-4)^2+(y-4)^2=16`